트리(Tree)
트리 자료구조란 마치 나무를 뒤집어 놓은 형태와 비슷하다고 해서 붙여진 이름이다.
트리는 그래프의 하위 집합인데, 트리가 되기 위해서는 조건이 필요하다.
트리의 조건
1. 컴포넌트가 하나인 연결 그래프이다.
2. 방향을 무시하였을 때, 싸이클이 존재하지 않는다.

위의 사진을 보면 오른쪽 그래프들은 모두 싸이클이 형성되어있다는 것을 알 수 있다.
즉, 트리가 아니다.
또한 트리가 1, 2 조건을 만족하게 되면
트리의 간선 개수는 트리의 모든 정점 개수보다 1이 작다.
라는 규칙도 발견할 수 있다.
트리의 구조

루트: 가장 상위의 노드.
서브트리: 작은 트리의 집합.
부모: 두 노드가 있을 때, 깊이가 작은 쪽의 노드.
자식: 두 노드가 있을 때, 깊이가 큰 쪽의 노드.
형제자매: 같은 부모 노드를 둔 서로 다른 자식 노드들의 관계.
리프 노드: 자식이 하나도 없는 노드.
트리의 중요한 성질은,
트리는 재귀적인 구조를 띈다는 것.
트리 순회 방법(Tree Traversal)
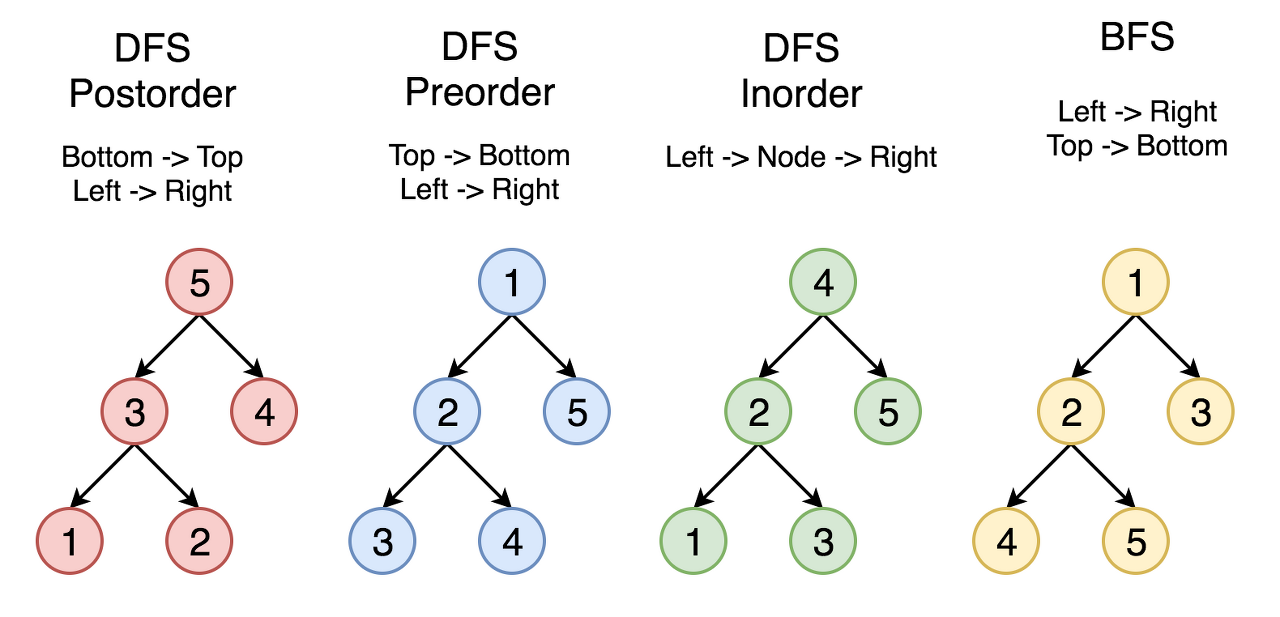
1. DFS
전위 순회(Pre-Order Traversal)
- 루트를 먼저 방문한 후에 자식들을 방문한다.
중위 순회(In-Order Traversal)
- 자식들 중간에 루트를 방문한다.
- 정의가 명확하지 않으므로, 이진 트리에서만 사용된다.
후위 순회(Post-Order Traversal)
- 자식들부터 모두 방문하고 루트를 방문한다.
2. BFS
레벨 순회(Level-Order Traversal)
- 그래프에서의 BFS와 같다.
*이진 트리(Binary Tree) : 차수가 최대 2인 트리를 이진 트리라고 한다.
'Computer Science > 자료구조' 카테고리의 다른 글
| [비선형구조] 그래프(Graph) (0) | 2023.05.18 |
|---|---|
| [선형구조] 큐(Queue), 덱(Deque) (0) | 2023.05.18 |
| [선형구조] 스택(Stack) (0) | 2023.05.18 |
| [선형구조] 리스트(List), 배열(Array), 연결 리스트(Linked List) (0) | 2023.05.18 |
| 자료구조 개요 (0) | 2023.05.18 |



